Bunch of Ideas, a little bit of Maths.

I am mathematician doing market research and data science

23 minute read

TASK 1

Soal

By using bisection method, find the root of the following functions:

  1. f(x) = x^2 - 3x - 2
  2. f(x) = x^3 + x^2 - 3x - 2

Jawab

Pada metode bisection, pemilihan selang iterasi menjadi penting. Berdasarkan teorema nilai antara:

Misalkan f \in C[a,b] dan L adalah suatu nilai di antara f(a) dan f(b). Maka ada suatu nilai c \in (a,b) yang memenuhi f(c) = L.

Oleh karena itu, kita perlu menemukan selang awal iterasi [a,b] yang memenuhi f(a).f(b)<0.

Iterasi akan dihentikan saat error memenuhi nilai yang diinginkan. Saya menggunakan kriteria pemberhentian iterasi sebagai berikut:

b_n-a_n < 10^{-5},n=1,2,..,I

Berikut adalah function metode bisection yang saya buat di R:

bagi_dua = function(a,b,f,iter_max,tol_max){
   # fungsi hitung bisection
    # initial condition
    i = 1
    hasil = data.frame(n_iter = NA,
                       a = NA,
                       b = NA,
                       c = NA)

    while(i<= iter_max && (b-a) > tol_max){
      # cari titik tengahnya
      p = a + ((b-a)/2)
      # hitung fungsi di titik tengah
      FP = f(p)
      # hitung fungsi di titik awal
      FA = f(a)
      # hitung fungsi di titik akhir
      FB = f(b)
      # tulis hasil dalam data frame
      hasil[i,] = list(i,a,b,p)
      
      # tukar nilai a atau b dengan nilai p 
      if(FA*FP < 0){b = p} else{a = p}
      # untuk iterasi berikutnya
      i  = i + 1
      
      # mencatat akar persamaan
      akar = p
      # tambahin dulu checking apakah f(a), f(b),atau f(c) ada yang nol?
      if(FP == 0){
        akar = p
        break} else if(FA == 0){
          akar = a
          break} else if(FB == 0){
            akar = b
            break}
      
    }
  
  # mencatat iterasi terbesar
  iterasi = i-1 # dikurang satu karena pada i+1 
                # sebenarnya tidak ada proses jika pada while TRUE
  
  # membuat ouput
  hasil = list(
    `iterasi max` = iterasi,
    `akar persamaan` = akar,
    `hasil perhitungan` = hasil
    )
  
  # print output
  return(hasil)
}

Persamaan I

Pertama-tama, mari kita buat grafik dari f(x) = x^2 - 3x - 2 sebagai berikut:

Dari grafik di atas, terlihat bahwa f(x) memiliki dua akar sebagai berikut:

  1. Satu akar f(x) berada di selang [-1,0].
  2. Satu akar f(x) lainnya berada di selang [3,4].

Berdasarkan informasi di atas, kita akan lakukan metode bisection di kedua selang tersebut.

Bisection pada selang [-1,0]

Berikut adalah hasil proses bisection di selang tersebut:

$`iterasi max`
[1] 17

$`akar persamaan`
[1] -0.5615463

$`hasil perhitungan`
   n_iter          a          b          c
1       1 -1.0000000  0.0000000 -0.5000000
2       2 -1.0000000 -0.5000000 -0.7500000
3       3 -0.7500000 -0.5000000 -0.6250000
4       4 -0.6250000 -0.5000000 -0.5625000
5       5 -0.5625000 -0.5000000 -0.5312500
6       6 -0.5625000 -0.5312500 -0.5468750
7       7 -0.5625000 -0.5468750 -0.5546875
8       8 -0.5625000 -0.5546875 -0.5585938
9       9 -0.5625000 -0.5585938 -0.5605469
10     10 -0.5625000 -0.5605469 -0.5615234
11     11 -0.5625000 -0.5615234 -0.5620117
12     12 -0.5620117 -0.5615234 -0.5617676
13     13 -0.5617676 -0.5615234 -0.5616455
14     14 -0.5616455 -0.5615234 -0.5615845
15     15 -0.5615845 -0.5615234 -0.5615540
16     16 -0.5615540 -0.5615234 -0.5615387
17     17 -0.5615540 -0.5615387 -0.5615463

Bisection pada selang [3,4]

Berikut adalah hasil proses bisection di selang tersebut:

$`iterasi max`
[1] 17

$`akar persamaan`
[1] 3.561546

$`hasil perhitungan`
   n_iter        a        b        c
1       1 3.000000 4.000000 3.500000
2       2 3.500000 4.000000 3.750000
3       3 3.500000 3.750000 3.625000
4       4 3.500000 3.625000 3.562500
5       5 3.500000 3.562500 3.531250
6       6 3.531250 3.562500 3.546875
7       7 3.546875 3.562500 3.554688
8       8 3.554688 3.562500 3.558594
9       9 3.558594 3.562500 3.560547
10     10 3.560547 3.562500 3.561523
11     11 3.561523 3.562500 3.562012
12     12 3.561523 3.562012 3.561768
13     13 3.561523 3.561768 3.561646
14     14 3.561523 3.561646 3.561584
15     15 3.561523 3.561584 3.561554
16     16 3.561523 3.561554 3.561539
17     17 3.561539 3.561554 3.561546

Kesimpulan

f(x) memiliki akar pada x = -0.5615463 dan x = 3.561546

Persamaan II

Pertama-tama, mari kita buat grafik dari f(x) = x^3 + x^2 - 3x - 2 sebagai berikut:

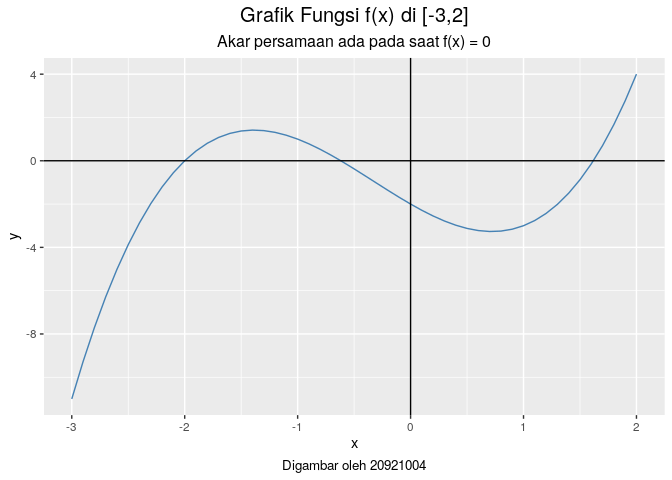
Dari grafik di atas, terlihat ada tiga akar persamaan di selang:

  1. [-3,-1]
  2. [-1,0]
  3. [1,2]

Berdasarkan informasi di atas, kita akan lakukan metode bisection di ketiga selang tersebut.

Bisection pada selang [-3,-1]

Berikut adalah hasil proses bisection di selang tersebut:

$`iterasi max`
[1] 1

$`akar persamaan`
[1] -2

$`hasil perhitungan`
  n_iter  a  b  c
1      1 -3 -1 -2

Bisection pada selang [-1,0]

Berikut adalah hasil proses bisection di selang tersebut:

$`iterasi max`
[1] 17

$`akar persamaan`
[1] -0.6180344

$`hasil perhitungan`
   n_iter          a          b          c
1       1 -1.0000000  0.0000000 -0.5000000
2       2 -1.0000000 -0.5000000 -0.7500000
3       3 -0.7500000 -0.5000000 -0.6250000
4       4 -0.6250000 -0.5000000 -0.5625000
5       5 -0.6250000 -0.5625000 -0.5937500
6       6 -0.6250000 -0.5937500 -0.6093750
7       7 -0.6250000 -0.6093750 -0.6171875
8       8 -0.6250000 -0.6171875 -0.6210938
9       9 -0.6210938 -0.6171875 -0.6191406
10     10 -0.6191406 -0.6171875 -0.6181641
11     11 -0.6181641 -0.6171875 -0.6176758
12     12 -0.6181641 -0.6176758 -0.6179199
13     13 -0.6181641 -0.6179199 -0.6180420
14     14 -0.6180420 -0.6179199 -0.6179810
15     15 -0.6180420 -0.6179810 -0.6180115
16     16 -0.6180420 -0.6180115 -0.6180267
17     17 -0.6180420 -0.6180267 -0.6180344

Bisection pada selang [1,2]

Berikut adalah hasil proses bisection di selang tersebut:

$`iterasi max`
[1] 17

$`akar persamaan`
[1] 1.618034

$`hasil perhitungan`
   n_iter        a        b        c
1       1 1.000000 2.000000 1.500000
2       2 1.500000 2.000000 1.750000
3       3 1.500000 1.750000 1.625000
4       4 1.500000 1.625000 1.562500
5       5 1.562500 1.625000 1.593750
6       6 1.593750 1.625000 1.609375
7       7 1.609375 1.625000 1.617188
8       8 1.617188 1.625000 1.621094
9       9 1.617188 1.621094 1.619141
10     10 1.617188 1.619141 1.618164
11     11 1.617188 1.618164 1.617676
12     12 1.617676 1.618164 1.617920
13     13 1.617920 1.618164 1.618042
14     14 1.617920 1.618042 1.617981
15     15 1.617981 1.618042 1.618011
16     16 1.618011 1.618042 1.618027
17     17 1.618027 1.618042 1.618034

Kesimpulan

f(x) memiliki akar pada x = -2, x = -0.6180344, dan x = 1.618034.

TASK 2

Soal

By using numerical integration, find the area under the following curve:

Jawab

Lingkaran I

Kita akan hitung terlebih dahulu untuk luas lingkaran pertama.

Perhatikan bahwa kita bisa membentuk kurva tersebut dengan fungsi f(x) = \sqrt{6^2 - x^2} \text{, untuk x } \in [0,6].

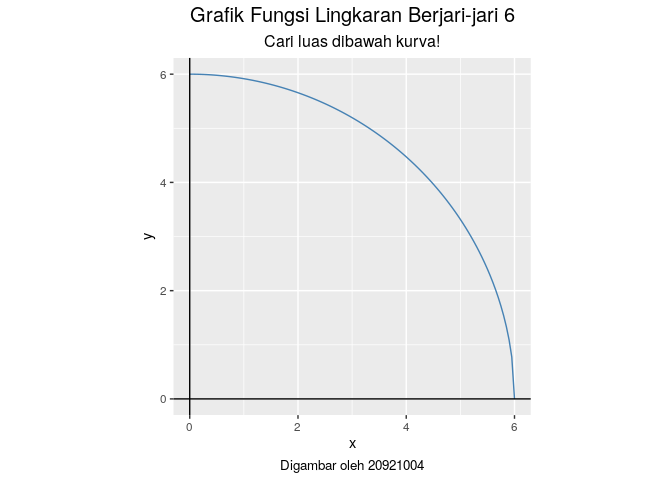
Untuk menghitung luas f(x) di [0,6] secara exact, setidaknya kita bisa melakukan dua hal, yakni:

  1. Menghitung \int_0^6{f(x)} dx.
  2. Menghitung dari rumus luas lingkaran: \frac{1}{4} \pi.r^2 = \frac{1}{4} \pi.6^2 = 28.2743339.

Untuk menghampirinya secara numerik, kita akan hitung penjumlahan luas dari square atau trapezoid yang dibangun di bawah kurva.

Berikut adalah function yang dibuat di R untuk kedua metode tersebut:

hampiri = function(x0,xn,n,f){
  # save initial dulu
  initial_1 = x0
  initial_2 = xn
  
  # ================================
  # metode square
  h = (xn - x0) / n
  integration = f(x0)
  for(i in 1:n){
    k = x0 + i*h
    integration = integration + f(k)
  }
  square = integration * h
  
  # =================================
  # metode trapezoid
  x0 = initial_1
  xn = initial_2
  h = (xn - x0) / n
  integration = f(x0) + f(xn)
  for(i in 1:n){
    k = x0 + i*h
    integration = integration + 2*f(k)
  }
  trapezoid = integration * h/2

  # =================================
  # bikin output
  selang = n
  luas_persegi = square
  luas_trapezoid = trapezoid
  
  output = list(selang,luas_persegi,luas_trapezoid)
}

Sekarang kita akan hitung luas f(x) untuk berbagai macam nilai n kemudian akan kita bandingkan hasilnya dengan hitungan exact sebelumnya.

Saya definisikan:

\Delta = \text{exact} - \text{hampiran}

n luas_persegi luas_trapezoid delta_persegi_exact delta_trapezoid_exact
5 30.93344 27.33344 -2.6591056 0.9408944
10 29.74066 27.94066 -1.4663311 0.3336689
25 28.90977 28.18977 -0.6354329 0.0845671
50 28.60442 28.24442 -0.3300827 0.0299173
100 28.44375 28.26375 -0.1694194 0.0105806
200 28.36059 28.27059 -0.0862586 0.0037414
500 28.30939 28.27339 -0.0350534 0.0009466
1000 28.29200 28.27400 -0.0176653 0.0003347
3000 28.28027 28.27427 -0.0059356 0.0000644
5000 28.27790 28.27430 -0.0035701 0.0000299
10000 28.27612 28.27432 -0.0017894 0.0000106
20000 28.27523 28.27433 -0.0008963 0.0000037
50000 28.27469 28.27433 -0.0003591 0.0000009

Hasil Perhitungan Hampiran vs Exact Lingkaran I

Lingkaran II

Secara exact luas lingkarannya adalah \frac{3}{4} \pi 6^2 = 84.8230016.

Pada lingkaran berikutnya, kita akan membuat fungsi sebagai berikut:

g(y) = \left\\begin{matrix} -\sqrt{6^2 - y^2} \text{, untuk y } \in [-6,0] \ \sqrt{6^2 - y^2} \text{, untuk x } \in [-6,6] \end{matrix}\right.

Oleh karena luas merupakan nilai positif, maka untuk menghitungnya kita akan buat fungsinya menjadi |g(y)|. Akibatnya:

g(y) = \left\\begin{matrix} \sqrt{6^2 - y^2} \text{, untuk y } \in [-6,0] \ \sqrt{6^2 - y^2} \text{, untuk x } \in [-6,6] \end{matrix}\right.

Saya juga akan hitung \Delta hampiran terhadap exact dengan definisi yang sama.

n luas_persegi luas_trapezoid delta_persegi_exact delta_trapezoid_exact
5 92.80032 82.00032 -7.9773167 2.8226833
10 89.22199 83.82199 -4.3989932 1.0010068
25 86.72930 84.56930 -1.9062987 0.2537013
50 85.81325 84.73325 -0.9902482 0.0897518
100 85.33126 84.79126 -0.5082582 0.0317418
200 85.08178 84.81178 -0.2587759 0.0112241
500 84.92816 84.82016 -0.1051602 0.0028398
1000 84.87600 84.82200 -0.0529960 0.0010040
3000 84.84081 84.82281 -0.0178068 0.0001932
5000 84.83371 84.82291 -0.0107102 0.0000898
10000 84.82837 84.82297 -0.0053682 0.0000318
20000 84.82569 84.82299 -0.0026888 0.0000112
50000 84.82408 84.82300 -0.0010772 0.0000028

Hasil Perhitungan Hampiran vs Exact Lingkaran II

TASK 3

Soal

Based on the following differential equation:

\frac{d}{dt}y(t) = t \sqrt{y(t)}; y(0)=1

Define y(t) for t = 0,1,2,..,10 by using 4th order Runge-Kutta! Use h=0.1.

Compare the result with the following exact solution:

y(t) = \frac{1}{16}(t^2+4)^2

Jawab

Untuk menjawabnya, pertama-tama kita akan buat function Runge-Kutta di R sebagai berikut:

rk_4order = function(f, x0, y0, h, n){
  # initial condition
  x = x0
  y = y0
  # proses iterasi
  for(i in 1:n){
    k1 = f(x0,y0)
    k2 = f(x0 + 0.5*h,y0 + 0.5*k1*h)
    k3 = f(x0 + 0.5*h,y0 + 0.5*k2*h)
    k4 = f(x0 + h,y0 + k3*h)
    y0 = y0 + (1/6)*(k1 + 2*k2 + 2*k3 + k4) * h
    x0 = x0 + h
    x = c(x, x0)
    y = c(y, y0)
  }
  # output
  output = data.frame(x = x,
                      y = y)
  return(output)
}

Sekarang kita akan hitung bagaimana hasilnya:

dydt = function(t,y){t * sqrt(y)}
y0 = 1
t0 = 0
h = 0.1
n = 100

hampiran = 
  rk_4order(f = dydt, 
            x0 = t0, 
            y0 = y0, 
            h = h, 
            n = n)

Lalu akan saya bandingkan hasilnya dari perhitungan exact dan menghitung \Delta = numerik - exact berikut:

t y_numerik y_exact delta
0.0 1.000000 1.000000 0.00e+00
0.1 1.005006 1.005006 0.00e+00
0.2 1.020100 1.020100 0.00e+00
0.3 1.045506 1.045506 0.00e+00
0.4 1.081600 1.081600 0.00e+00
0.5 1.128906 1.128906 0.00e+00
0.6 1.188100 1.188100 0.00e+00
0.7 1.260006 1.260006 -1.00e-07
0.8 1.345600 1.345600 -1.00e-07
0.9 1.446006 1.446006 -1.00e-07
1.0 1.562500 1.562500 -1.00e-07
1.1 1.696506 1.696506 -2.00e-07
1.2 1.849600 1.849600 -2.00e-07
1.3 2.023506 2.023506 -3.00e-07
1.4 2.220100 2.220100 -3.00e-07
1.5 2.441406 2.441406 -4.00e-07
1.6 2.689599 2.689600 -5.00e-07
1.7 2.967006 2.967006 -6.00e-07
1.8 3.276099 3.276100 -7.00e-07
1.9 3.619505 3.619506 -8.00e-07
2.0 3.999999 4.000000 -9.00e-07
2.1 4.420505 4.420506 -1.10e-06
2.2 4.884099 4.884100 -1.20e-06
2.3 5.394005 5.394006 -1.40e-06
2.4 5.953598 5.953600 -1.60e-06
2.5 6.566404 6.566406 -1.70e-06
2.6 7.236098 7.236100 -2.00e-06
2.7 7.966504 7.966506 -2.20e-06
2.8 8.761598 8.761600 -2.40e-06
2.9 9.625504 9.625506 -2.60e-06
3.0 10.562497 10.562500 -2.90e-06
3.1 11.577003 11.577006 -3.20e-06
3.2 12.673597 12.673600 -3.50e-06
3.3 13.857003 13.857006 -3.80e-06
3.4 15.132096 15.132100 -4.10e-06
3.5 16.503902 16.503906 -4.40e-06
3.6 17.977595 17.977600 -4.70e-06
3.7 19.558501 19.558506 -5.10e-06
3.8 21.252094 21.252100 -5.50e-06
3.9 23.064000 23.064006 -5.80e-06
4.0 24.999994 25.000000 -6.20e-06
4.1 27.066000 27.066006 -6.60e-06
4.2 29.268093 29.268100 -7.10e-06
4.3 31.612499 31.612506 -7.50e-06
4.4 34.105592 34.105600 -7.90e-06
4.5 36.753898 36.753906 -8.40e-06
4.6 39.564091 39.564100 -8.80e-06
4.7 42.542997 42.543006 -9.30e-06
4.8 45.697590 45.697600 -9.80e-06
4.9 49.034996 49.035006 -1.03e-05
5.0 52.562489 52.562500 -1.08e-05
5.1 56.287495 56.287506 -1.13e-05
5.2 60.217588 60.217600 -1.19e-05
5.3 64.360494 64.360506 -1.24e-05
5.4 68.724087 68.724100 -1.30e-05
5.5 73.316393 73.316406 -1.36e-05
5.6 78.145586 78.145600 -1.41e-05
5.7 83.219992 83.220006 -1.47e-05
5.8 88.548085 88.548100 -1.53e-05
5.9 94.138490 94.138506 -1.60e-05
6.0 99.999983 100.000000 -1.66e-05
6.1 106.141489 106.141506 -1.72e-05
6.2 112.572082 112.572100 -1.79e-05
6.3 119.300988 119.301006 -1.86e-05
6.4 126.337581 126.337600 -1.92e-05
6.5 133.691386 133.691406 -1.99e-05
6.6 141.372079 141.372100 -2.06e-05
6.7 149.389485 149.389506 -2.13e-05
6.8 157.753578 157.753600 -2.20e-05
6.9 166.474483 166.474506 -2.28e-05
7.0 175.562477 175.562500 -2.35e-05
7.1 185.027982 185.028006 -2.43e-05
7.2 194.881575 194.881600 -2.50e-05
7.3 205.133980 205.134006 -2.58e-05
7.4 215.796073 215.796100 -2.66e-05
7.5 226.878879 226.878906 -2.74e-05
7.6 238.393572 238.393600 -2.82e-05
7.7 250.351477 250.351506 -2.90e-05
7.8 262.764070 262.764100 -2.99e-05
7.9 275.642975 275.643006 -3.07e-05
8.0 288.999968 289.000000 -3.16e-05
8.1 302.846974 302.847006 -3.24e-05
8.2 317.196067 317.196100 -3.33e-05
8.3 332.059472 332.059506 -3.42e-05
8.4 347.449565 347.449600 -3.51e-05
8.5 363.378870 363.378906 -3.60e-05
8.6 379.860063 379.860100 -3.69e-05
8.7 396.905968 396.906006 -3.79e-05
8.8 414.529561 414.529600 -3.88e-05
8.9 432.743966 432.744006 -3.98e-05
9.0 451.562459 451.562500 -4.07e-05
9.1 470.998465 470.998506 -4.17e-05
9.2 491.065557 491.065600 -4.27e-05
9.3 511.777463 511.777506 -4.37e-05
9.4 533.148055 533.148100 -4.47e-05
9.5 555.191360 555.191406 -4.57e-05
9.6 577.921553 577.921600 -4.67e-05
9.7 601.352958 601.353006 -4.78e-05
9.8 625.500051 625.500100 -4.88e-05
9.9 650.377456 650.377506 -4.99e-05
10.0 675.999949 676.000000 -5.10e-05

Hasil Perhitungan Exact vs Numerik (RK4)

Terlihat bahwa \Delta yang didapatkan sudah sangat kecil, yang berarti perhitungan secara exact dan numerik sudah sangat dekat (akurat).

You May Also Enjoy

Geocoding di R Menggunakan tidygeocoder

7 minute read

Di blog ini saya sudah menuliskan berbagai macam metode dan teknik pengambilan data longlat dari alamat (vice versa). Istilah kerennya itu geocoding.